nanaxfood.blogg.se

1. BIPOLAR SQUARE WAVE MATHEMATICAL REPRESENTATION SERIES TO APPROXIMATE
2. BIPOLAR SQUARE WAVE MATHEMATICAL REPRESENTATION CODE UP THE

The PWM waveform is basically a square wave, with a frequency we will define as. It has pretty simple mathematics that allow us to plot ripple voltage.We can see from the graph that `f(t + π) = - f(t)`.In theory a square wave has an instantaneous rise and fall. Example: This Square Wave: L (the Period is 2 ) The square wave is from h to +h Now our job is to calculate a 0, a n and b n. A 0 is the net area between L and L, then divided by 2L. It is basically an average of f(x) in that range.

Bipolar Square Wave Mathematical Representation Series To Approximate

Mathematical models that represent the inverter allow us to.If we now move `π` units to the right (or about `2 + 3.14 = 5.14`),This same behaviour will occur for any value of `t` thatThis means that in our Fourier expansion we will only see terms like the following:`f(t)=(a_0)/2+(a_1\ cos t + b_1\ sin t)` ` +\ (a_3\ cos 3t + b_3\ sin 3t)` ` +\ (a_5\ cos 5t+ b_5\ sin 5t)+.`[ Note: Don't be confused with odd functions and odd harmonics. Clearly , this area is less for a sinusoid than for a square wave ( the latter indeed giving the maximum theoretical power achievable as the full available. Π 2π 3π 4π 5π −π 0.5π -0.5π t f(t) Open image in a new pageSquare Wave Don Johnson This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 1.0 Abstract Shows how to use ourierF series to approximate a square wave, as opposed to the sinusoidal waves seen previously.

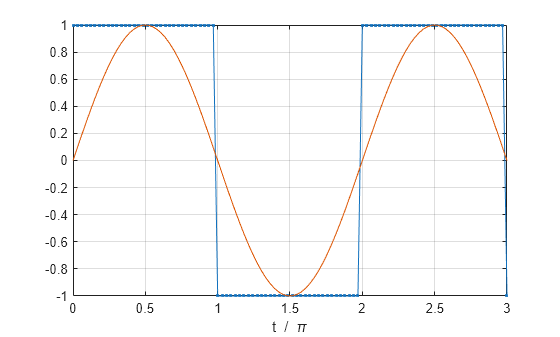
Bipolar Square Wave Mathematical Representation Code Up The

What we will need to do before hand is declare what our frequency is. But how in the world would you do that? Welcome to the world of the Symbolic Math Toolbox. Therefore, f = 1 means that we repeat our square wave every second.Basically, what you have to do is code up the first line of the equation. Recall that the frequency is the amount of cycles per seconds. I won't bother you with the details, but you can represent any periodic function as a summation of cosines and sines (à la Without going into the derivation, this is the closed-form equation for a square wave of frequency f, with a peak-to-peak amplitude of 2 (i.e.

In this case, x is just that. Try it yourself: syms x Syms denotes that you are declaring anything coming after the statement to be a mathematical variable. You can then use diff to differentiate and see what the derivative is. A good example would be if you want to use this to define a closed-form solution of a function f(x). After, MATLAB has a whole suite of tools that you can use to evaluate functions that rely on these variables. With the Symbolic Math Toolbox, you can define what are considered as mathematics variables within MATLAB.

We can do this by: syms t k FuncSum = (sin(2*pi*(2*k - 1)*f*t) / (2*k - 1)) That settles that problem. Once we do this, we need to create our function that is inside the summation first. We see that there are in fact two variables in the periodic square function that need to be defined: t and k. Cool eh? In any case, let's get back to our problem at hand.

In our case, that's infinity, and so MATLAB has a special keyword called Inf to denote that. Start is the beginning of the sum, which is 1 in our case, and finish is where we wish to finish up our summation. V is the summation variable that we wish to use to index in the sum. We usually call it like this: funcOut = symsum(func, v, start, finish) Func is the function we wish to sum over. If you want to symbolically sum over a function, we must use the symsum function.

However, you'll see that at the points where the wave repeats itself, we get NaN values and so there is a disconnect between the high peak and low peak. As such, simply chop off the complex parts to get the real parts only: yout = real(double(yout)) %// To cast back to double.You could also do this the ezplot way by doing: ezplot(xsquare). Also, because the Fourier Series is generally a complex-valued function, and the square-wave is purely real, the output of this function will actually give you a complex-valued vector. Let's just choose 1 for now. As such, we can fill this in using either 1 or -1.

Either way, I wanted to give a more signal processing perspective to how to do this. I was still writing this post by the time he put something up.